I. Principe global▲
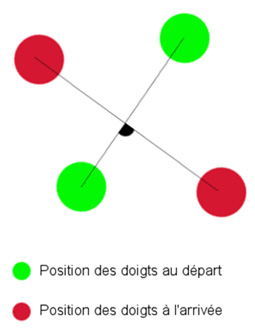
On souhaite reconnaître un mouvement de rotation effectué avec deux doigts pour par exemple inverser deux fragments positionnés l'un en dessous de l'autre comme indiqué sur l'image ci-dessous.
Concrètement, nous allons enregistrer les coordonnées de départ et d'arrivée de nos deux doigts puis calculer l'angle formé par ceux-ci, comme indiqué dans le schéma ci-dessous. Dans notre cas, si l'angle mesuré est supérieur à 8 ° (par exemple), la rotation s'effectue.
II. Algorithme▲
On détecte lorsque plusieurs doigts sont posés sur l'écran puis on sauvegarde les coordonnées des points touchés. Lorsque les doigts sont enlevés, on enregistre également leurs coordonnées.
On calcule ensuite le point d'intersection I de la droite formée par les deux doigts au départ et de celle formée à l'arrivée. Appelons A le point de départ du doigt 1 et B son point d'arrivée. L'étape suivante consiste à calculer les distances des côtés du triangle ABI. Comme on possède les coordonnées de ces points, il ne reste qu'à utiliser la formule :
AB= (xA - xB)² + (yB - y1)² , où A (xA, yA) et B (xB, yB)
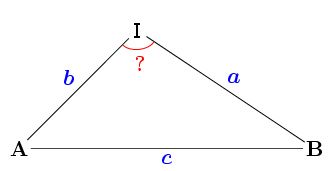
Enfin, pour calculer l'angle en radian, on utilise le théorème d'Al Kashi (ou théorème de Pythagore généralisé) dont la formule est la suivante :
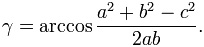
III. Implémentation Java : quelques pistes▲
Premièrement, il faut placer un listener sur votre layout principal, celui qui fait la taille de la page et qui contient tous les éléments. C'est lui qui captera l'événement.
mainLayout.setOnTouchListener(new View.OnTouchListener() {
@Override
public boolean onTouch(View view, MotionEvent motionEvent) {
int pointerIndex = ((motionEvent.getAction() & MotionEvent.ACTION_POINTER_ID_MASK) >> MotionEvent.ACTION_POINTER_ID_SHIFT);
int action = (motionEvent.getAction() & MotionEvent.ACTION_MASK);
int pointCnt = motionEvent.getPointerCount();
try {
// On effectue un traitement seulement lorsque deux doigts touchent l'écran
if ((pointCnt == 2)&& (pointerIndex <=1)){
switch (action) {
case MotionEvent.ACTION_POINTER_DOWN:
// Sauvegarde des coordonnées de départ des deux doigts
for (int i = 0; i < pointCnt; i++) {
int id = motionEvent.getPointerId(i);
//simple exemple de comment récupérer les coordonnées des points. Celles-ci doivent être traitées en fonction de ce que l'on veut faire
float x= motionEvent.getX(i)
float y= motionEvent.getY(i));
}
break;
case MotionEvent.ACTION_POINTER_UP:
// Sauvegarde des coordonnées des doigts lorsque l'utilisateur les enlève de l'écran
for (int i = 0; i < pointCnt; i++) {
int id = motionEvent.getPointerId(i);
//simple exemple de comment récupérer les coordonnées des points. Celles-ci doivent être traitées en fonction de ce que l'on veut faire
float x= motionEvent.getX(i)
float y= motionEvent.getY(i));
}
//calculer ici la valeur de l'angle formé, comme expliqué dans le paragraphe précédent
break;
default:
break;
}
}
} catch (Exception e) {
Log.e("error", e.getMessage());
}
return true;
}
});IV. Conclusion▲
En espérant que ce tutoriel vous soit utile pour la compréhension du multi-touch. Vous avez maintenant toutes les cartes en main pour l'implémenter !
V. Remerciements▲
Je tiens à remercier tout particulièrement Feanorin qui a mis ce tutoriel au format Developpez.com.
Merci également à ClaudeLELOUP et ced d'avoir pris le temps de le relire et de le corriger.